Esse garotinho lindo ai é o meu filho Leon Eduardo, (Postado por Jesus Américo Couto Corrêa).
Esse garotinho lindo ai é o meu filho Leon Eduardo, (Postado por Jesus Américo Couto Corrêa).
sexta-feira, 12 de dezembro de 2008
quinta-feira, 11 de dezembro de 2008
Texto do Lucas
 Eu apreciei bastante a realização do projeto da criação dos blogs pois é uma maneira diferente e divertida de fazer os trabalhos de matemática.
Eu apreciei bastante a realização do projeto da criação dos blogs pois é uma maneira diferente e divertida de fazer os trabalhos de matemática.(postado por Lucas Soares dos Santos) F
Texto do Jesus Américo
 Pra mim a idéia do Trabalho no Blog foi muito legal, ainda mais pra mim, eu que adoro trabalhar com computadores, e o trabalho excelente para aquelas pessoas que adoram computadores e detestam caderno, foi um trabalho muito legal, eu até que no começo achei que seria muito difícil, mas depois percebi que era legal fazer os trabalhos de Matemática no computador é completamente mais fácil do que no caderno, nós da Turma 301 do C.I.E.P. de Bagé em 2008 conhecemos um novo jeito mais divertido de fazer Trabalhos de Matemática, foi muito legal, espero que a professora Grace siga com o projeto do Blog de Matemática com a nova 300 no ano que vem (2009), Até mais amigos. (postado por Jesus Américo Couto Corrêa).
Pra mim a idéia do Trabalho no Blog foi muito legal, ainda mais pra mim, eu que adoro trabalhar com computadores, e o trabalho excelente para aquelas pessoas que adoram computadores e detestam caderno, foi um trabalho muito legal, eu até que no começo achei que seria muito difícil, mas depois percebi que era legal fazer os trabalhos de Matemática no computador é completamente mais fácil do que no caderno, nós da Turma 301 do C.I.E.P. de Bagé em 2008 conhecemos um novo jeito mais divertido de fazer Trabalhos de Matemática, foi muito legal, espero que a professora Grace siga com o projeto do Blog de Matemática com a nova 300 no ano que vem (2009), Até mais amigos. (postado por Jesus Américo Couto Corrêa).Geometria Analítica
Vamos agora mostrar atividades sobre Geometria Analítica
do site da UNIJUI
Primeira Questão:
Quando movimentamos uma única reta varia o coeficiente angular e linear da mesma,e quando movimentamos o ponto de intersecção varia o coeficiente linear das equações de todas as retas e as coordenadas do ponto de intersecção.
Segunda Questão:
Quando movimentamos o ponto Q concluímos que quanto maior o ângulo de inclinação da reta maior o coeficiente angular e quanto menor o ângulo de inclinação da reta menor o coeficiente angular (para ângulos agudos).
Em relação ao ponto de intersecção da reta com o eixo das ordenadas e o coeficiente linear da equação da reta concluímos que ambos possuem o mesmo valor.
Terceira Questão:
O que existe em comum nas equações de duas retas paralelas e que as duas possuem o mesmo coeficiente angular.
Quarta Questão:
Retas perpendiculares: Para encontrarmos o coeficiente angular de uma das retas basta calcular-mos o inverso do simétrico do valor do coeficiente angular dado pela outra reta.
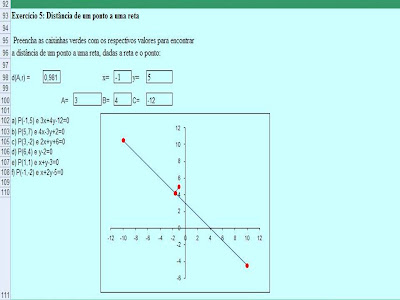
Quinta Questão:
Exercícios do Excel:

sexta-feira, 26 de setembro de 2008
Fractais

A geometria fractal � o ramo da matem�tica que estuda as propriedades e comportamento dos fractais. Descreve muitas situa�es que n�o podem ser explicadas facilmente pela geometria cl�ssica, e foram aplicadas em ci�ncia, tecnologia e arte gerada por computador. As ra�zes conceituais dos fractais remontam a tentativas de medir o tamanho de objetos para os quais as defini�es tradicionais baseadas na geometria euclidiana falham.
Um fractal (anteriormente conhecido como curva monstro) � um objeto geom�trico que pode ser dividido em partes, cada uma das quais semelhante ao objeto original. Diz-se que os fractais t�m infinitos detalhes, s�o geralmente auto-similares e independem de escala. Em muitos casos um fractal pode ser gerado por um padr�o repetido, tipicamente um processo recorrente ou iterativo.
O termo foi cunhado em 1975 por Beno�t Mandelbrot, matem�tico franc�s nascido na Pol�nia, que descobriu a geometria fractal na d�cada de 70 do s�culo XX, a partir do adjetivo latino fractus, do verbo frangere, que significa quebrar.
segunda-feira, 18 de agosto de 2008
PARABENS CIEP
Trasendo educação e alegria para muitas crianças e adolesentes.
segunda-feira, 7 de julho de 2008
CONSTRUÇÃO DE POLIEDROS



Foi realizado em sala de aula a construção de poliedros.